If ever you have a dataset with percentile rank as a column, it’s tempting to do common analytical techniques on this column because it’s easy to interpret and most people have basic understanding and intuition regarding this 0 to 100 range. Analytics software makes averages on a column very easy, but it turns out that it’s a bad idea to do this and will regularly lead to incorrect conclusions. Doing basic math on percentile ranks might seem like it should work, but in reality math operations like adding, subtracting, or averaging all result in inaccurate results when you use percentile rank as if it were a unit of measure.
To help you understand why the stakes of this analytical mistake are high, imagine you teach at a school that offers a bonus for any teacher whose students improve (on average) by 10 percentiles from their prior year state tests. While this might seem a fair measure, it’s fundamentally flawed such that some teachers will have a much harder time attaining this goal, and it turns out that taking averages of percentiles is mathematically illegal. The good news is that there’s an easy fix: use Normal Curve Equivalents (NCEs) instead of percentile rank, and there’s an easy excel formula to do your conversion. We hope you’ll find this video helpful and it’ll help you do the right things with your data! In a hurry? You’re also welcome to watch the abbreviated version here.
Watched the video? Read Nate and Peter’s summary / remix below to ensure you’re ready to apply it to your own data.
Education is a consequential field that ends up generating a lot of data in any given academic year, but understanding education data can be complex. School and district leaders want to measure success, and they want to know what to do after they analyze the data. It’s common for them to want to know things like which classrooms are seeing more or less success in growing students. Since standardized tests might change year to year and people don’t always have good access to rigorous growth norms, one of the easiest ways to see if students are growing is to compare their current percentile rank to an earlier one (typically at the end of the prior school year). For example, a student who ranked at the 45th percentile last year (performed better than 45% of all students taking the test) but is at the 61st percentile rank this year has grown a lot: not only have they kept pace with their peers and grown the typical amount this year, they have made more than a typical year of growth and have passed some of their peers in the process. Even if the tests themselves were of different difficulty levels or offered by different testing vendors we can identify their progress year over year just by looking at the change in percentile rank.
Because comparing percentile ranks is easy and these ranks are included in many datasets, it’s not uncommon to see someone subtract the current year’s percentile rank from the previous year’s to assess how much students grew or regressed relative to the “typical growth” of peers starting at the same incoming achievement. They may also take averages of those percentile ranks before subtracting, producing something like this:
| Teacher | Spring 2022 Average Pctl. Rank | Spring 2023 Average Pctl. Rank | Growth |
| Teacher A | 11 | 22 | +11 |
| Teacher B | 35 | 37 | +2 |
| Teacher C | 48 | 59 | +11 |
| Teacher D | 90 | 94 | +4 |
Based on the chart above, a principal could come to the conclusion that teachers A and C are achieving phenomenal growth, and teachers B and D should perhaps be mentored by them to learn what techniques and approaches contribute to such great academic achievement.
However, this analysis is based on a faulty model. This is because percentile ranks are not created equal. Instead, they are distributed unevenly based on the achievement of the students in the sample set. For most valid and age-appropriate tests, student achievement will resemble a bell curve or normal distribution, like this:
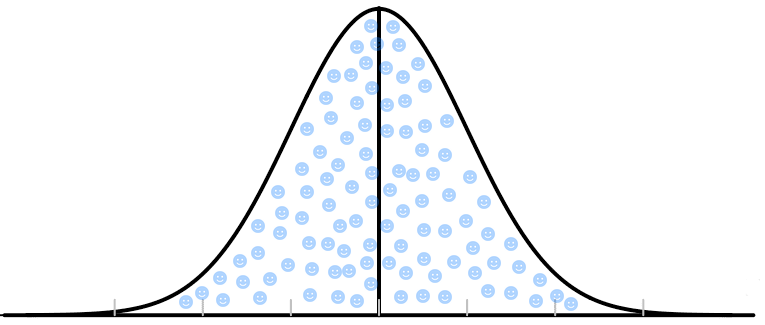
You can imagine each blue circle/face as 1 out of 100 typical students. A student with percentile rank 50 is about in the middle as they have 50 students scoring lower than them. A student performing at the 3rd percentile will have 3 students scoring lower than them.
Most of the students will achieve test scores near the middle of the distribution, with relatively fewer getting the lowest or highest test scores. A helpful analogy is to think of a cross country race or a marathon. If you watch a large race from the finish line, the fastest runner often comes in well ahead of the second fastest. Then, the next few fastest runners will cross the finish line individually, typically with noticeable gaps in between them. Following this, the main body of runners will show up, with many average runners crossing the finish line in quick succession. At the tail end will come the slower runners, once again separated typically by larger and larger gaps between them, with the final runner or two lagging significantly behind the next slowest runner. If your coach challenged you to pass 10 runners and move up your percentile rank by 10 at the next race, where would you rather be? In the back of the pack, the middle, or right near the front?
A runner at the very back of the pack or near the front would need to cut their time significantly more than a runner in the middle in order to pass an equal number of runners. This same logic applies to standardized test results. A student near the very bottom or the very top of the achievement distribution needs to improve their score by a lot more than a student in the middle to result in an equal increase in percentile rank. Herein lies the central reason why any sort of arithmetic done on percentile ranks is invalid: the unit of 1 percentile rank doesn’t exist and isn’t a unit at all. It’s small in some places, and much larger in others. It’s not like all the other numbers in your life where a dollar is a dollar or a degree of Fahrenheit is a degree of Fahrenheit.
What is a principal, education data practitioner or teacher to do when they want to analyze a dataset that only includes percentile ranks? The answer is deceptively simple, and revolves around a statistical conversion developed within the education data world called a Normal Curve Equivalent, or NCE.
| Excel/Google Sheets Formula to Convert Percentile Rank (PR) to NCE | Excel/Google Sheets Formula to Convert NCE to Percentile Rank (PR) |
| =21.06*NORMSINV(PR/100)+50 | =100*NORMSDIST((NCE-50)/21.06) |
It turns out that NCEs are similar to percentile ranks and they are anchored to each other in three places such that 1 NCE = 1 Percentile Rank (PR), 50 NCE = 50 PR, and 99 NCE = 99 PR. Everywhere in between, they have been rescaled or standardized to be what mathematicians calls “equal interval.” This means that growth of 10 NCE is about the same difficulty at all places on the scale. A student growing from the 1st NCE to the 11st NCE is about as noteworthy as from the 50th to the 60th. This is not true for percentiles.
Converting percentile ranks to NCEs is useful in a variety of ways. NCEs allow someone wanting to subtract (find the difference) or average growth scores to do so without making a big analytical mistake. They also allow for an analyst to compare growth based on how challenging it likely was to achieve that growth. To return to the previous table of teachers’ growth scores, if we convert the percentile scores to NCEs, we get the following results.
| Teacher | Spring 2022 Average NCE | Spring 2023 Average NCE | NCE Growth |
| Teacher A | 24 | 34 | +10 |
| Teacher B | 42 | 43 | +1 |
| Teacher C | 49 | 55 | +6 |
| Teacher D | 77 | 83 | +6 |
With NCEs, this table now more accurately shows the relative above average effectiveness of each teacher. Remember that the percentile rank or NCE staying the same for a class of students is what we expect, so a teacher of average effectiveness would be expected to have a zero in the growth column. Each of these teachers appears to be growing students faster than typical, but Teacher A’s growth is the highest. We can now also see that teacher C and teacher D are roughly equally effective at driving student growth. Had we relied solely on percentiles, teacher D would likely have been frustrated and potentially even been set up for mentoring from someone with lower growth data. Additionally, if teachers were rewarded with merit-based pay for certain levels of growth, the NCE growth numbers are a fairer way to assess teachers’ effectiveness across different starting student ability levels.
There is one important caveat to using NCEs. The formula for conversion from percentile ranks to NCEs assumes normally distributed underlying data. The main time to be wary of this assumption is any time you believe a nontrivial portion of students in the tested population (across the state or the nation) are maxing out the test (scoring close to the max score) or scoring close to the minimum score of what you would get guessing on every question. In general, if it’s a valid and age-appropriate test with a large and diverse population to norm on, the percentile to NCE conversion will be approximately correct and certainly better than attempting to do differences or averages on percentile ranks.
United InfoLytics Loves Education Data
While we serve clients in a variety of industries, we are passionate about helping schools and districts understand their data and make valid conclusions from the analysis on that data. The right understanding helps lead to the right decisions, and ultimately this is good for the health of schools and the students they serve. Whether you need help with one-off data analysis or work to integrate your data systems while making analytics easier, we are happy to talk about your goals and where we can fit into your success.
